
Définir les meilleures
stratégies de prévision
Cette étude propose d’évaluer la valeur économique d’une prévision probabiliste de variables continues, une méthode utilisée dans deux nombreux domaines pour améliorer la prise de décision. Les études de cas réalisées sur le marché de l’énergie solaire démontrent un gain net significatif de la prévision probabiliste par rapport à la climatologie et à la prévision déterministe.
Par Josselin Le Gal La Salle (Laboratoire PIMENT, Université de la Réunion)
Cette recherche s’appuie sur le constat que dans de nombreux domaines (météorologie, finance, énergie, etc.), la simple prévision déterministe ne suffit pas pour optimiser la prise de décision. Dans ce cas, l’utilisation des prévisions probabilistes – qui caractérisent les évènements futurs par des probabilités – s’impose. Si la qualité (c‘est-à-dire la correspondance avec les observations) des prévisions probabilistes a été largement étudiée, leur valeur opérationnelle — c’est-à-dire le gain réel qu’un décideur peut tirer en les utilisant — l’est beaucoup moins, surtout quand la variable à prévoir est continue. Jusqu’à présent, la plupart des travaux se sont concentrés sur la valeur des prévisions probabilistes d’événements binaires (de la forme oui/non ; par exemple, va-t-il pleuvoir ou non demain ?). Le cadre développé ne s’applique pas directement aux variables continues (comme le niveau de production d’énergie, la demande, des flux mesurables).
Ce travail s’attache alors à proposer une méthodologie permettant d’évaluer la valeur économique d’une prévision probabiliste de variables continues. L’objectif est de proposer un cadre méthodologique robuste, relié au cadre binaire bien établi, mais adapté aux variables continues, et capable de prendre en compte la structure de coût d’un décideur réel. Nous proposons ici une méthodologie permettant de caractériser la valeur d’une prévision probabiliste dans le cas où l’utilisateur prend une décision à l’aide de la prévision (par exemple, un volume de vente), et où le coût pour l’utilisateur est linéaire par rapport à l’écart (la “déviation”) entre la décision et la réalisation.

Une méthodologie nouvelle est proposée pour évaluer la valeur des prévisions probabilistes quand la variable prédite est continue, sous l’hypothèse que les fonctions de coût (pertes liées aux décisions) sont linéaires par morceaux (“market-based loss functions”). Dans ce contexte, nous démontrons que deux indicateurs clés gouvernent la prise de décision optimale :
- R, le “risk ratio” : il correspond au ratio entre deux coefficients de pente : celui des coûts (pertes) quand la décision est supérieure à la mesure et celui des coûts lorsqu’elle est inférieure ;
- γ, la somme des pentes, qui caractérise le “niveau de risque” associé à une décision.
Nous montrons que la décision optimale (c.-à-d. le réglage de la variable à décider) correspond à un quantile P de la distribution prédite (P=R) et qu’il existe un lien formel entre la perte économique effective (la “vraie” perte qu’un décideur subit) et le pinball loss, utilisé dans les scores de quantile : la perte effective est proportionnelle au pinball loss (donc au “quantile score”), avec un facteur γ.
Afin d’utiliser ce lien, nous introduisons :
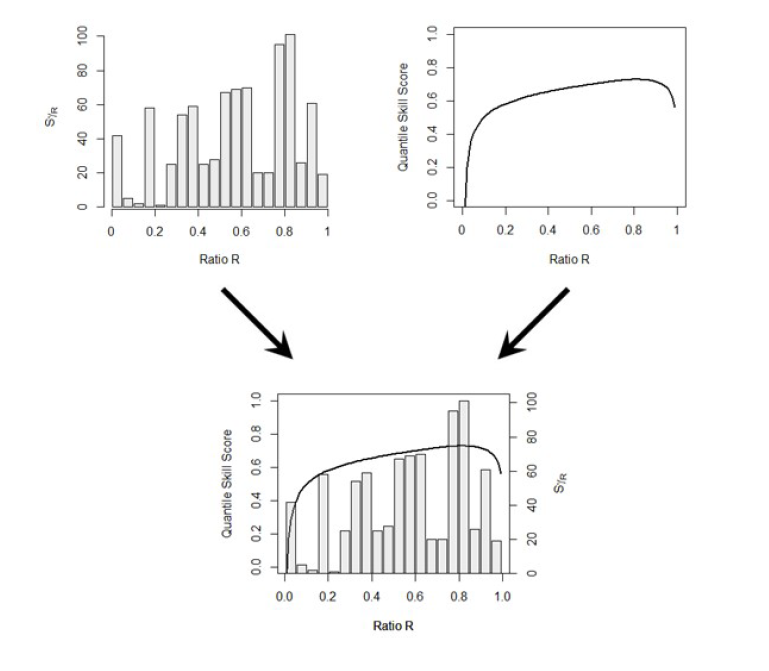
- Le diagramme des scores de quantile (« quantile score diagram ») : il trace le quantile score selon les niveaux de quantile (τ entre 0 et 1), reflétant la qualité de la prévision pour chaque quantile. Il caractérise uniquement la performance de la prévision, hors de tout contexte d’utilisation.
- Le diagramme de distribution du risque (« risk distribution diagram ») : il montre, sur l’axe des ratios R, la somme des γ (risques) associés à chaque R à partir de l’historique des décisions, ce qui illustre quelles zones de R sont les plus “coûteuses” ou critiques pour l’utilisateur. Il caractérise complètement la structure des coûts caractérisant le contexte d’utilisation des prévisions.
- Ensuite, la simple superposition de ces deux diagrammes définit le diagramme EVC (“Effective economic Value for Continuous variable”) : il permet de visualiser, pour un usage spécifique, la valeur effective réelle d’un forecast, non seulement en termes de qualité prédictive, mais pondérée par l’importance des risques associés aux différentes valeurs de R.
Crédits : J. Le Gal La Salle
Une métrique quantitative, l’OEV (Overall Effective Value), qui est une moyenne pondérée du quantile skill score (QSS) par la distribution des risques (les S_γ) permet de quantifier la valeur de la prévision pour le cas d’usage.
Pour illustrer cette méthode, deux types d’applications sont ensuite étudiées :
- Simulation théorique : Des données d’observation fictives suivant des variables normales, puis plusieurs types de prévisions synthétiques (probabilistes “idéales”, “fine” ou “grossière”, “biaisées”, et déterministes) sont générées. En calculant les diagrammes EVC pour différentes distributions de risque (risque “constant”, “centré”, “extrême”, etc.), nous arrivons aux conclusions suivantes :
- Les prévisions probabilistes statistiquement bien calibrées obtiennent systématiquement la meilleure valeur (OEV la plus élevée).
- Les prévisions déterministes ou biaisées perdent beaucoup de valeur quand le risque est concentré dans des quantiles extrêmes, démontrant que l’intérêt des prévisions probabilistes dépend fortement de la structure de risque du décideur.
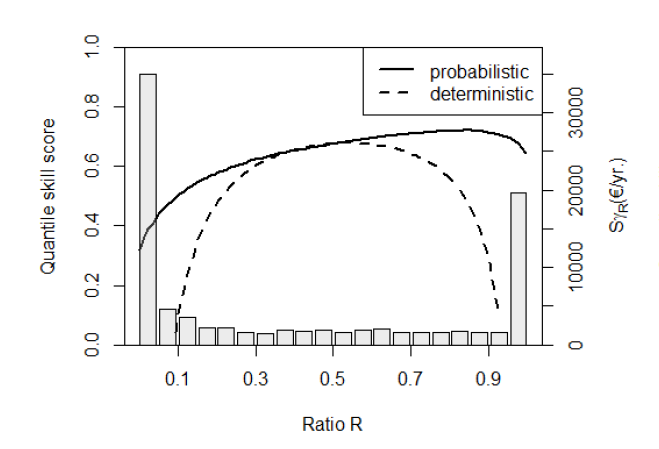
- Étude de cas réelle dans le marché de l’énergie solaire : Nous étudions ensuite la vente sur le marché « day-ahead » (J+1) de l’électricité produite par un parc photovoltaïque virtuel. Les prix de pénalité (ou « imbalance prices ») sont les prix réels constatés sur trois marchés européens (France, Portugal, Suisse). En appliquant des prévisions déterministes (moyenne d’un ensemble) et probabilistes (ensemble + correction de variance), nous calculons l’OEV via le diagramme EVC. Les résultats montrent que dans tous les marchés, la prévision probabiliste apporte un gain net significatif par rapport à la climatologie et à la prévision déterministe, particulièrement lorsque la distribution des risques (les pénalités) est extrême (par exemple en France). De plus, la valeur effective de la prévision probabiliste est plus robuste face aux variations de la structure de coût que celle de la prévision déterministe.
Crédits : J. Le Gal La Salle
En résumé, les résultats préliminaires montrent que cette méthodologie capture bien la valeur ajoutée des prévisions probabilistes continues, surtout quand les décisions sont sensibles aux queues de distribution (extrêmes), et que cette valeur peut être quantifiée de manière opérationnelle.
Quelles applications pour cette méthode ?
Pour l’industrie, la méthode permet aux décideurs (entreprises énergétiques, institutions financières, etc.) d’évaluer quantitativement la valeur ajoutée des prévisions probabilistes dans des contextes concrets, non seulement en termes d’erreur prédictive, mais en intégrant leur structure de coût réelle. Cela peut guider les investissements dans les systèmes de prévision probabiliste, justifier leur adoption face à des prévisions déterministes, et aider à optimiser les stratégies décisionnelles (par exemple sur les marchés d’énergie, les assurances, la gestion des risques).
Pour la recherche en prévision, le cadre proposé peut devenir un standard pour l’évaluation de la “valeur économique” des prévisions continues, en prolongeant le paradigme bien établi du cost–loss pour les événements binaires. De plus, le lien formel entre le quantile score (une métrique de qualité) et la perte économique (via γ) ouvre la porte à des optimisations de modèles qui visent non seulement à améliorer la précision, mais aussi à maximiser la valeur.
Plusieurs perspectives futures découlent de cette méthode :
- Étendre le cadre à des fonctions de coût non linéaires ou plus complexes que les coûts linéaires par morceaux (actuels), car dans la réalité, les pertes peuvent avoir des formes plus compliquées.
- Prendre en compte l’incertitude sur les paramètres de coût en intégrant l’apprentissage de ces paramètres par les décideurs.
- Appliquer la méthode à d’autres secteurs (assurance, finance, santé) pour valider sa généralité et évaluer la robustesse de l’OEV dans des contextes différents.
- Travailler sur la communication des probabilités et des risques aux utilisateurs finaux pour qu’ils utilisent pleinement la valeur apportée.
A Set of New Tools to Measure the Effective Value of Probabilistic Forecasts of Continuous Variables
Josselin Le Gal La Salle, Mathieu David, Philippe Lauret.
Forecasting, 2025, 7,
https://doi.org/10.3390/forecast7020030
Cette publication entre dans le cadre du projet Fine4Cast, piloté par Georges Kariniotakis. L’objectif principal du projet Fine4Cast est d’améliorer la prévision à court terme (quelques minutes à quelques jours) de la production d’énergies renouvelables (EnR) et de la consommation à une échelle géographique fine (centrales de production, consommacteurs, territoires).
Fine4Cast propose une approche holistique qui couvre toute la chaîne de valeur et de modélisation de la prévision énergétique, allant des données aux prévisions météorologiques et énergétiques, et incluant l’utilisation optimale des prévisions pour la prise de décision dans les systèmes électriques et le marché de l’énergie.
Plus d'actualités Publication


